Calculate Z-Score in Excel: Easy Guide
Understanding and applying statistical methods like the Z-Score can provide significant insights into datasets, enabling better data-driven decisions in various fields such as finance, marketing, and research. Excel, with its powerful tools, offers an intuitive platform for calculating Z-Scores, allowing analysts to transform raw data into standardized scores quickly. This blog post will delve into how to calculate the Z-Score in Excel with detailed steps, providing you with a comprehensive guide that simplifies this statistical computation.
Why Use Z-Scores?
Before diving into the calculation, it’s essential to understand why Z-Scores are useful:
- To compare scores from different datasets: Z-Scores standardize different distributions for comparison.
- For quality control: Identifying outliers or anomalies in data.
- In research: To normalize data for statistical tests.
The Formula
The formula for calculating the Z-Score of a value, X, in a dataset is:
Z = (X - μ) / σ
- X is the individual data point.
- μ is the mean of the dataset.
- σ is the standard deviation of the dataset.
Step-by-Step Guide to Calculate Z-Score in Excel
Preparing Your Data
First, ensure your data is in a single column or row for ease of calculation:
- Input your data into an Excel spreadsheet. For instance, let’s assume your data is in column A from row 2 to 51 (
A2:A51).
Calculating the Mean (μ)
To find the mean:
- In an empty cell, enter the formula for the AVERAGE function:
=AVERAGE(A2:A51) - This will give you the mean (μ) of your dataset.
Calculating the Standard Deviation (σ)
To compute the standard deviation:
- In another empty cell, type:
=STDEV.P(A2:A51)for the population standard deviation or=STDEV.S(A2:A51)for the sample standard deviation. - Depending on whether you are analyzing a sample or the entire population, choose the appropriate function. STDEV.P is for the entire population, while STDEV.S is for a sample.
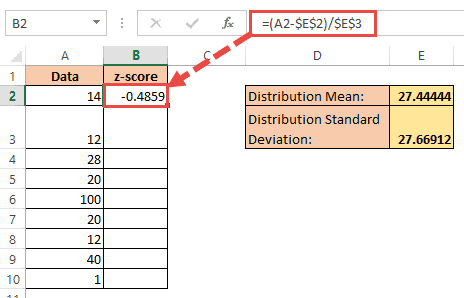
Computing the Z-Score
Now, to calculate the Z-Score for each value in your dataset:
- Choose a cell adjacent to your data, let’s say B2.
- Enter the formula:
=(A2-AVERAGE(A2:A51))/STDEV.S(A2:A51) - Drag the formula down the column to fill the rest of the cells, calculating the Z-Score for each data point.
Interpreting Z-Scores
Here’s how to interpret Z-Scores:
- Positive Z-Score: The value is above the mean.
- Negative Z-Score: The value is below the mean.
- Z-Score of 0: The value is exactly at the mean.
- The magnitude indicates how many standard deviations the value is from the mean.
Common Misinterpretations and Limitations
Here are some considerations:
- Z-Scores assume a normal distribution, which might not always be the case.
- Extreme values or outliers can significantly affect the Z-Score, potentially leading to misinterpretation.
- Data transformation into Z-Scores can lose original context, making it less intuitive for some analyses.
📌 Note: Always ensure your dataset's distribution before applying Z-Score analysis for more accurate results.
By following this guide, you now possess the tools to calculate Z-Scores in Excel, offering you the ability to normalize data for comparison or quality control. Understanding and interpreting Z-Scores can reveal deeper insights into your data, allowing for more informed decision-making. The simplicity of Excel's functions makes this statistical analysis accessible, even if you're not a seasoned statistician.
What if my data isn’t normally distributed?
+If your data isn’t normally distributed, the Z-Score might not be the best measure for standardizing or comparing values. Consider using other transformations or nonparametric methods for analysis.
Can I calculate Z-Scores for categorical data?
+Z-Scores are not suitable for categorical data since they require numerical values to compute. Instead, look into methods like chi-square tests for categorical data analysis.
How do I interpret Z-Scores in terms of standard deviations?
+A Z-Score tells you how many standard deviations a value is from the mean. For example, a Z-Score of 2 means the value is 2 standard deviations above the mean.
Related Terms:
- Z-score calculator
- Z score sample calculator
- Z-score table
- Z-score to percentile Excel
- Z-test calculator
- Z distribution Excel



